Teil 4: Das Additionswerk (schematischer Aufbau)
Schickard schrieb 1623 an Kepler: "...und eine Maschine konstruiert, die aus 11 vollständigen und 6 verstümmelten Rädchen besteht und mit gegebenen Zahlen sofort selbsttätig rechnet, sie addiert, subtrahiert, multipliziert und dividiert..."
Bis zu diesem Zeitpunkt waren keine mechanische Rechenmaschine bekannt. Um so höher ist Schickards Leistung einzuschätzen, der scheinbar mühelos eine Lösung für den kritischen Zehnerübertrag fand, denn erschreibt auch: " ... wie sie die linken Stellen bei Überschreitung des Zehners oder Hunderters von selbst erhöht oder bei der Subtraktion ihnen etwas fortnimmt...". Maschinen anderer Konstrukteure, die Jahrzehnte später erschienen, verfügten nur über einen unvollständigen bzw. unzuverlässigen Zehnerübertrag oder ließen ihn nur in einer Drehrichtung zu, was bei der Subtraktion die Arbeit mit gegensinnigen, roten Zahlen erfordert. Der Zehnerübertrag per dekadischem Zahnrad hat enge Fertigungstoleranzen, welche die damaligen Fertigungstechniken in der Regel nicht erlaubten. Selbst die leibniz'sche Maschine konnte erst später, als präzise Restaurationen möglich waren, volle Funktionstüchtigkeit erlangen.
Folgt man den technisch-mechanischen Überlegungen, die bei der ersten Rekonstruktion in Tübingen angestellt wurden, gibt es immer noch verschiedene räumliche Anordungen des schickard'schen Zehner-Übertragungsweges. Der Übertrag erfolgt von rechts (Einerstelle) nach links. Die drei unterschiedlichen Übertragungsräder, wie sie in der tübinger Lösung und in weiteren Replica verwendet werden, sind ab hier farbig markiert.
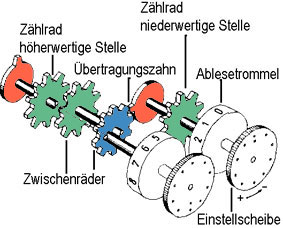 Zum besseren Überblick ist rechts die bereits erwähnte dreidimensionale Darstellung eingefärbt. Die verschiedenen Zahnradtypen sind hier auseinandergerückt, um den Übertragungsweg optisch zu verdeutlichen. Zum besseren Überblick ist rechts die bereits erwähnte dreidimensionale Darstellung eingefärbt. Die verschiedenen Zahnradtypen sind hier auseinandergerückt, um den Übertragungsweg optisch zu verdeutlichen.
 Um die von Schickard erwähnte Zahl von 11 + 6 Rädern nicht zu überschreiten, fasste man in der tübinger Version Typ A und Typ B (blau + grün) zusammen und zählte sie als eines. Es wurde ein dickes Rad gefertigt, dessen Zähne auf einer Seite zur Hälfte abgeschliffen waren (vgl. Abbildung auf Seite 3). Den gleichen Effekt erhält man, wenn man A und B aufeinander lötet. Es würde auch ausreichen, auf dem Typ A in Höhe der halben Zähne Stifte oder kleine Metallstücke zu befestigen, auf die der "Einzahn" C zugreift. Ebenso wäre es möglich, A und C zu verbinden, also auf A nur ein Stück Metall aufzubringen, das als Einzahn wirkt. Die von Schickard erwähnte Gesamtzahl von 17 Rädern erfordert nach der tübinger Lösung jedenfalls, entweder A und B oder aber A und C zu kombinieren bzw. als Kombination zu zählen. Um die von Schickard erwähnte Zahl von 11 + 6 Rädern nicht zu überschreiten, fasste man in der tübinger Version Typ A und Typ B (blau + grün) zusammen und zählte sie als eines. Es wurde ein dickes Rad gefertigt, dessen Zähne auf einer Seite zur Hälfte abgeschliffen waren (vgl. Abbildung auf Seite 3). Den gleichen Effekt erhält man, wenn man A und B aufeinander lötet. Es würde auch ausreichen, auf dem Typ A in Höhe der halben Zähne Stifte oder kleine Metallstücke zu befestigen, auf die der "Einzahn" C zugreift. Ebenso wäre es möglich, A und C zu verbinden, also auf A nur ein Stück Metall aufzubringen, das als Einzahn wirkt. Die von Schickard erwähnte Gesamtzahl von 17 Rädern erfordert nach der tübinger Lösung jedenfalls, entweder A und B oder aber A und C zu kombinieren bzw. als Kombination zu zählen.
Nachfolgend zunächst das Schema der tübinger Lösung, die A und B zu einem Rad zusammenfasst. Rad C wäre dann das "verstümmelte" Zahnrad, von dem Schickard 6 Stück erwähnt. Die 3D-Darstellung rechts findet sich in den Achsen 2 und 3 bzw. 4 und 5, wobei die Räder A und C auf der jeweils rechten Achse vertauscht sind. Danach folgen einige mögliche Variationen der Anordnung.
Bei den Abbildungen wurden der Übersicht halber nur die Achsen der Einstellräder gezeichnet. Typ C auf Achse 6 löst die0berlaufglocke aus, Typ A auf Achse 1 (bzw. 6) dient nur der Rasterfederung, also der präzisen Einstellung des Rades.
Tübinger Lösung

Die platzsparendste Lösung (nur 3 Ebenen)
(Man erkennt, dass auf einer der Zwischenachsen die Typen A und B getrennt montiert werden müssen.)

Sehr übersichtliche, lineare Anordnung, mit einer Ausnahme nur Doppelzahnräder, jedoch 6 Ebenen tief
(gebaut von Freddy Haeghens)
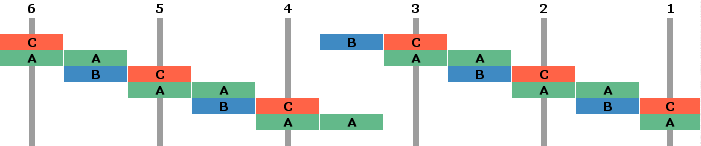
Das mag genügen, es gibt natürlich noch mehr Varianten. Einzige Bedingung ist die Abfolge der Zahnräder, wobei die horizontale Abfolge (immer von rechts nach links zu denken) zwingend ist, die Ebenen jedoch vertauscht sein können:
Mit diesem Thema haben sich alle mehr oder weniger gründlich beschäftigt, die eine Replica gebaut haben. Die mir bekannten Lösungen gehen davon aus, dass die drei oben beschriebenen Zahnrad-Typen A, B und C verwendet werden, auch wenn A und B oder A und C zu einem Stück zusammengefügt sind. Auf der nächsten Seite (5. Theoretische Alternativen) stelle ich etwas abweichende, jedoch deutlich einfachere Varianten vor, und danach einen alternativen Eigenbau.
|
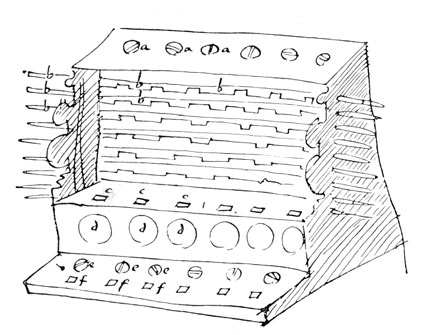
 Zum besseren Überblick ist rechts die
Zum besseren Überblick ist rechts die  Um die von Schickard erwähnte Zahl von 11 + 6 Rädern nicht zu überschreiten, fasste man in der tübinger Version Typ A und Typ B (blau + grün) zusammen und zählte sie als eines. Es wurde ein dickes Rad gefertigt, dessen Zähne auf einer Seite zur Hälfte abgeschliffen waren (vgl. Abbildung auf
Um die von Schickard erwähnte Zahl von 11 + 6 Rädern nicht zu überschreiten, fasste man in der tübinger Version Typ A und Typ B (blau + grün) zusammen und zählte sie als eines. Es wurde ein dickes Rad gefertigt, dessen Zähne auf einer Seite zur Hälfte abgeschliffen waren (vgl. Abbildung auf 

